
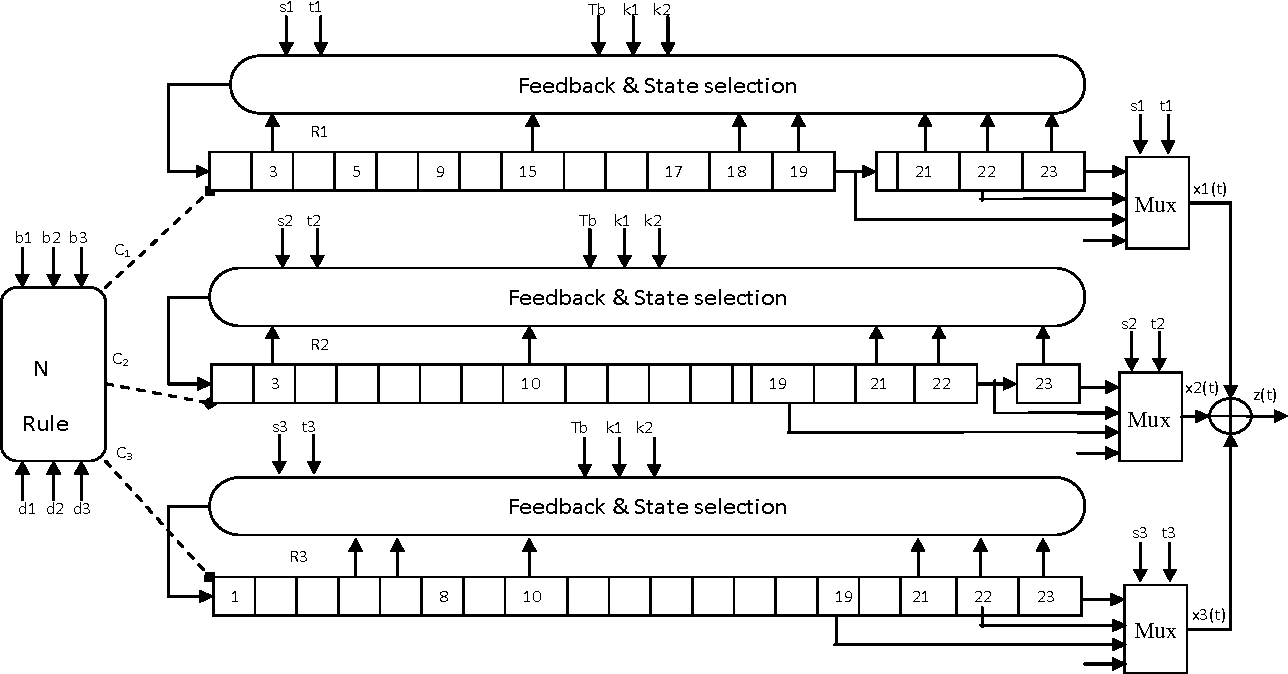
The polynomials are represented in bitwise little endian: Bit 0 (least significant bit) represents the coefficient of \(x^0\), bit \(k\) represents the coefficient of \(x^k\), etc. The implementation is optimized for clarity, not for speed. The duration of the linear feedback shift register (LFSR) in number of 'chips' is 2N-1 where N is the number of states in the shift register (and order of the generator polynomial), and chips refers to each unique output that is generated in the sequence. Pick a characteristic polynomial of some degree \(n\), where each monomial coefficient is either 0 or 1 (so the coefficients are drawn from \(\text\) modulo the characteristic polynomial equals \(x^0\).įor each \(k\) such that \(k < n\) and \(k\) is a factor of \(2^n - 1\), \(x^k\) modulo the characteristic polynomial does not equal \(x^0\). Linear Feedback Shift Registers © John Knight Dig Cir p. Its setup and operation are quite simple: Transcribed image text: A linear feedback shift register (LFSR) was discussed in class that had three D-flip-flops Qu.o connected in cascade in the order. Here we will focus on the Galois LFSR form, not the Fibonacci LFSR form. A linear feedback shift register (LFSR) is a mathematical device that can be used to generate pseudorandom numbers.


 0 kommentar(er)
0 kommentar(er)
